QQ扫一扫联系


百度百科诠释:
贝塞尔曲线(Bézier curve),又称贝兹曲线或贝济埃曲线,是应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线,贝兹曲线由线段与节点组成,节点是可拖动的支点,线段像可伸缩的皮筋,我们在绘图工具上看到的钢笔工具就是来做这种矢量曲线的。贝塞尔曲线是计算机图形学中相当重要的参数曲线,在一些比较成熟的位图软件中也有贝塞尔曲线工具,如PhotoShop等。在Flash4中还没有完整的曲线工具,而在Flash5里面已经提供出贝塞尔曲线工具。
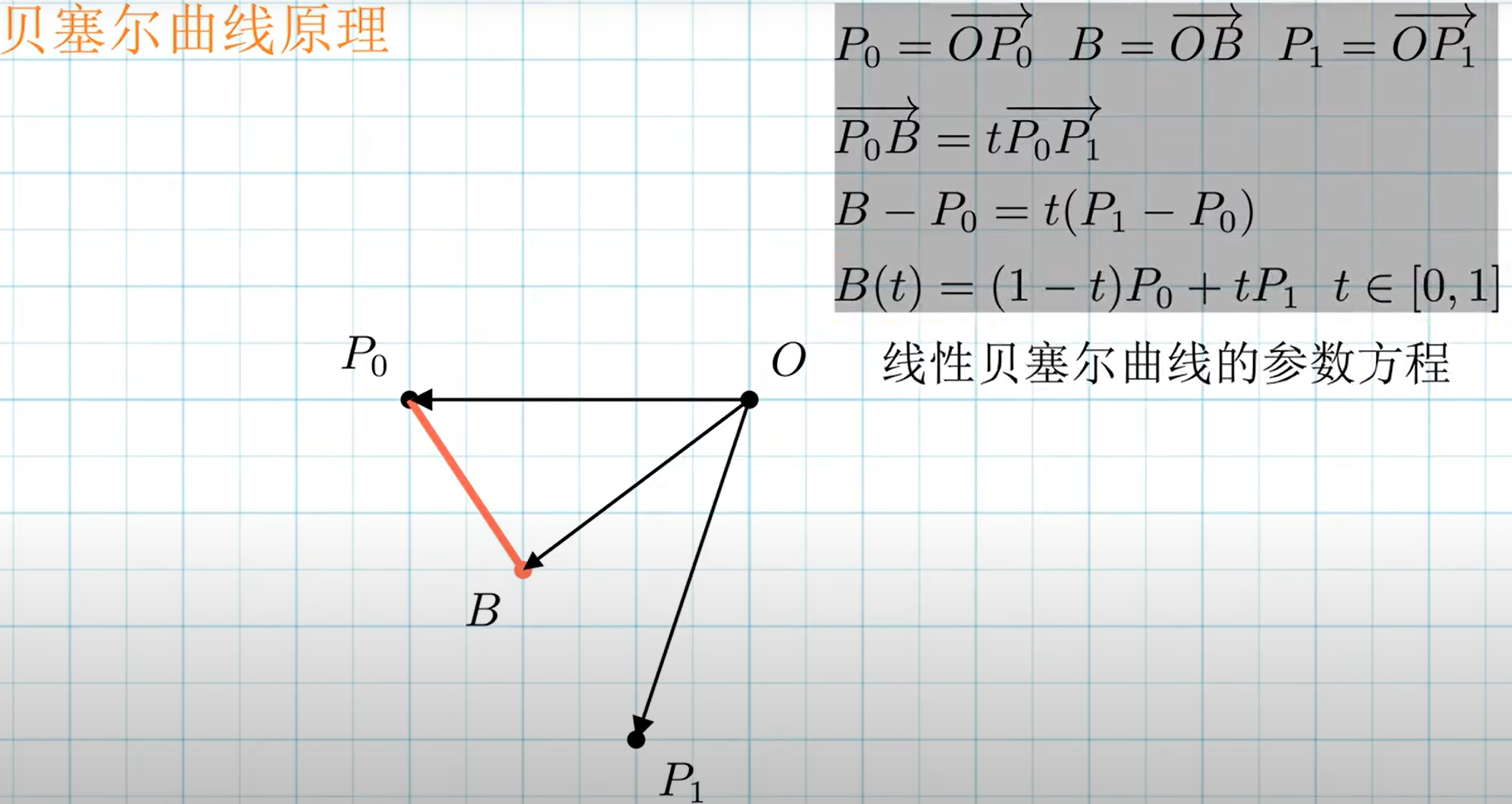
给定点P0、P1,线性贝兹曲线只是一条两点之间的直线。这条线由下式给出:
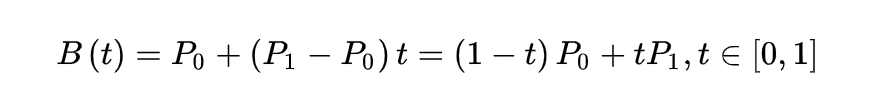
且其等同于线性插值。
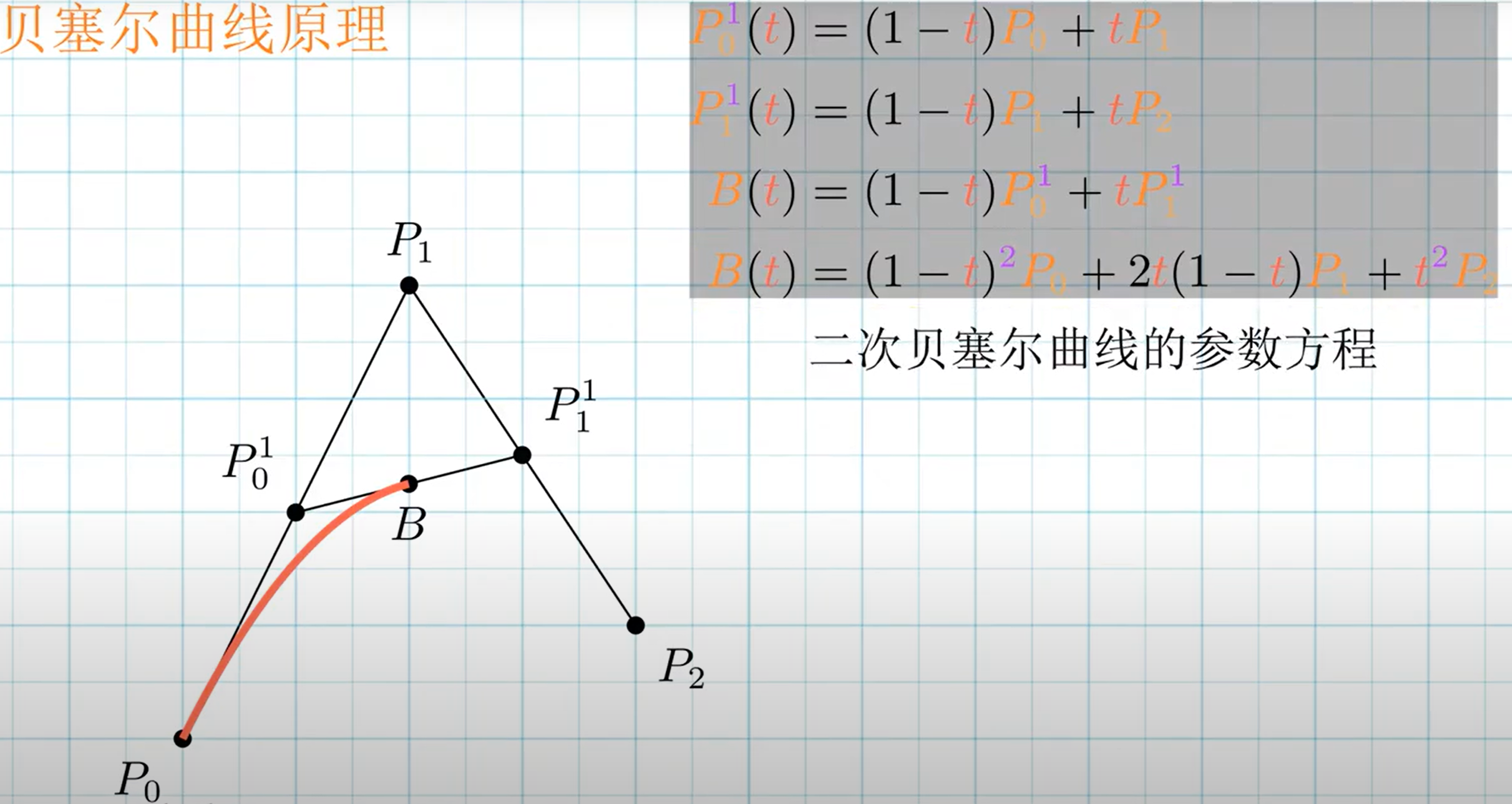
二次方贝兹曲线的路径由给定点P0、P1、P2的函数B(t)追踪:
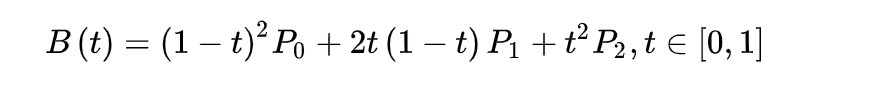
TrueType字型就运用了以贝兹样条组成的二次贝兹曲线。
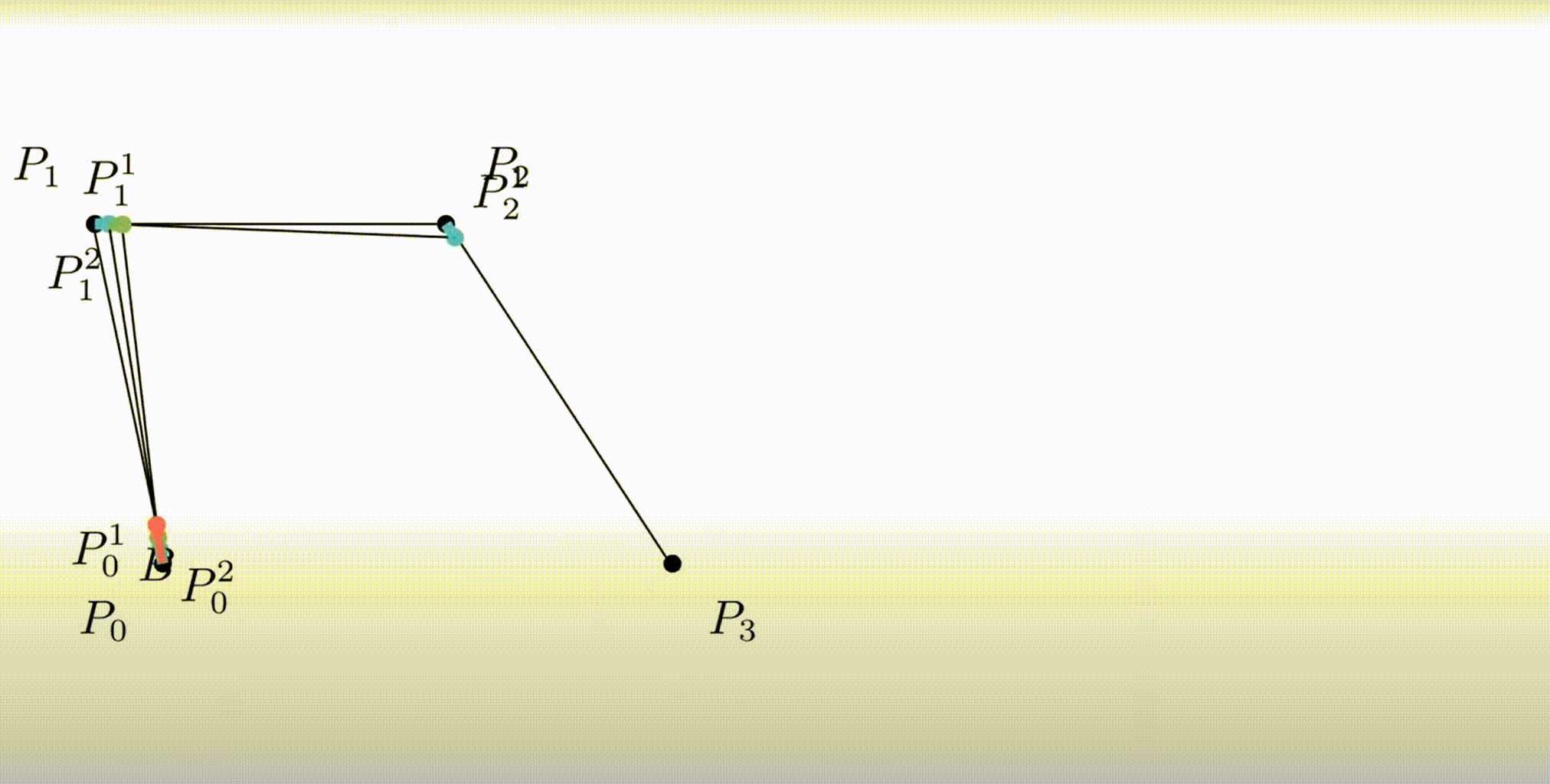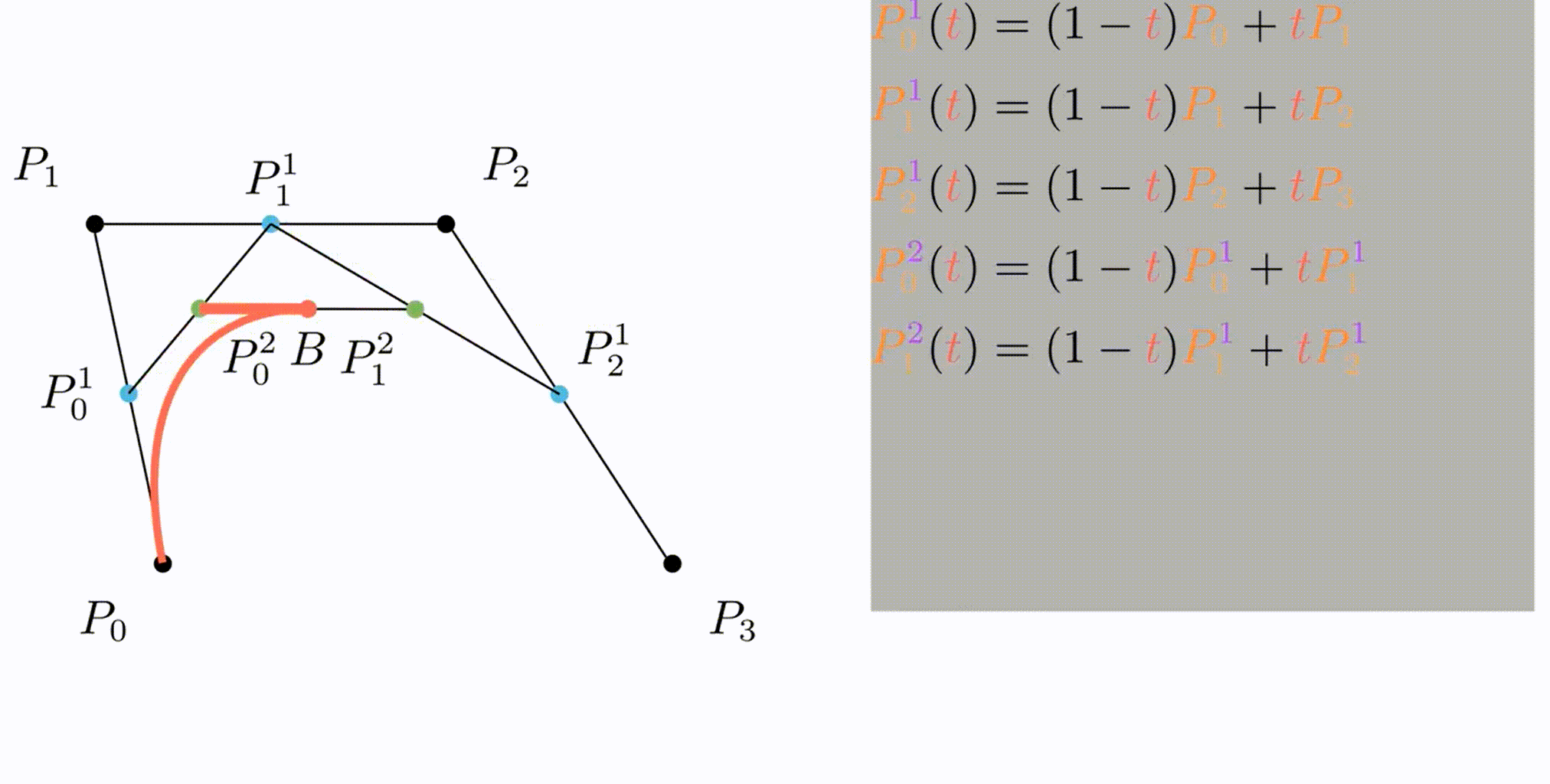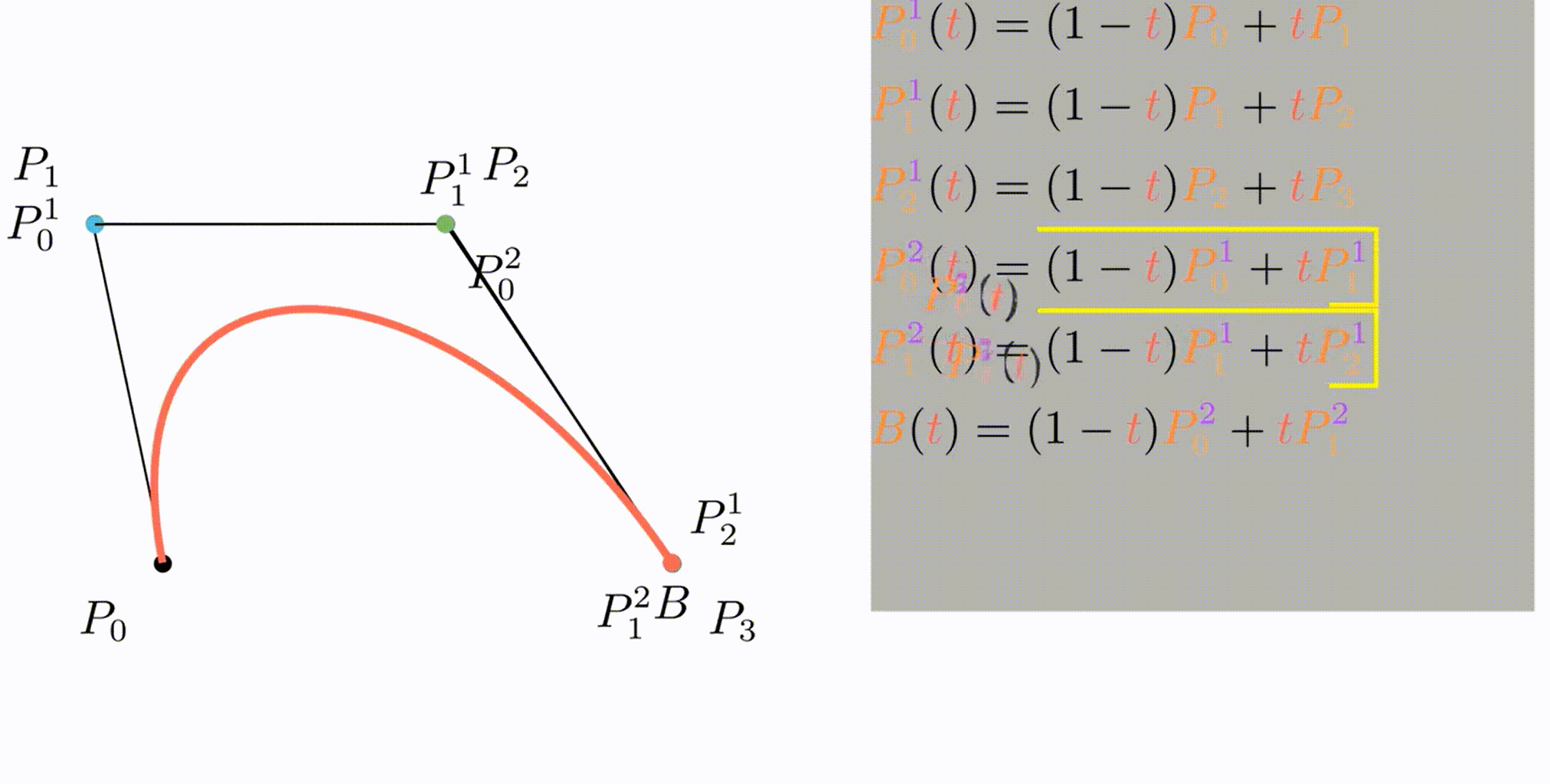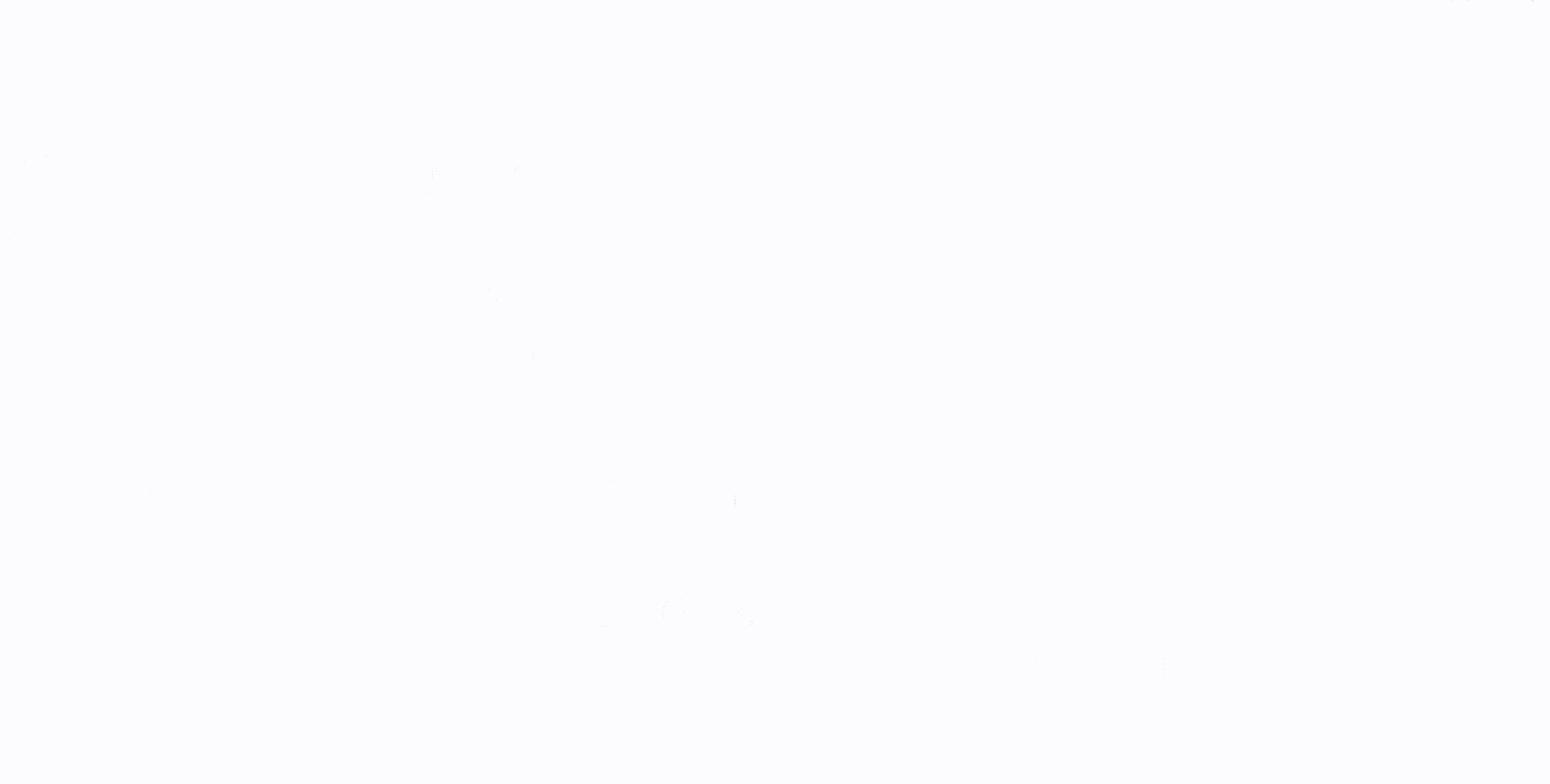
P0、P1、P2、P3四个点在平面或在三维空间中定义了三次方贝兹曲线。曲线起始于P0走向P1,并从P2的方向来到P3。一般不会经过P1或P2;这两个点只是在那里提供方向资讯。P0和P1之间的间距,决定了曲线在转而趋进P3之前,走向P2方向的“长度有多长”。
曲线的参数形式为:
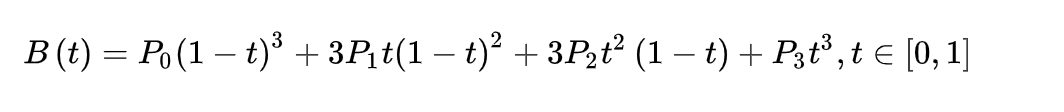
现代的成象系统,如PostScript、Asymptote和Metafont,运用了以贝兹样条组成的三次贝兹曲线,用来描绘曲线轮廓。
阶贝兹曲线可如下推断。给定点P0、P1、…、Pn,其贝兹曲线即:
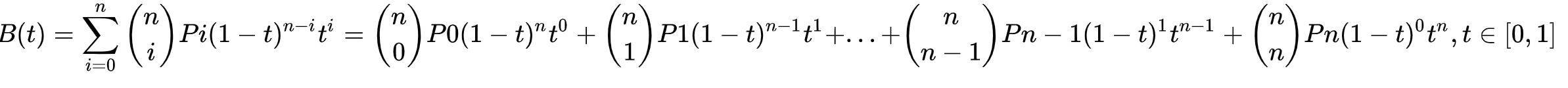
如上公式可如下递归表达: 用表示由点P0、P1、…、Pn所决定的贝兹曲线。
用平常话来说,阶的贝兹曲线,即双阶贝兹曲线之间的插值。
开始于P0并结束于Pn的曲线,即所谓的端点插值法属性。
曲线是直线的充分必要条件是所有的控制点都位在曲线上。同样的,贝塞尔曲线是直线的充分必要条件是控制点共线。
曲线的起始点(结束点)相切于贝塞尔多边形的第一节(最后一节)。
一条曲线可在任意点切割成两条或任意多条子曲线,每一条子曲线仍是贝塞尔曲线。
一些看似简单的曲线(如圆)无法以贝塞尔曲线精确的描述,或分段成贝塞尔曲线(虽然当每个内部控制点对单位圆上的外部控制点水平或垂直的的距离为时,分成四段的贝兹曲线,可以小于千分之一的最大半径误差近似于圆)。
位于固定偏移量的曲线(来自给定的贝塞尔曲线),又称作偏移曲线(假平行于原来的曲线,如两条铁轨之间的偏移)无法以贝兹曲线精确的形成(某些琐屑实例除外)。无论如何,现存的启发法通常可为实际用途中给出近似值。
public class BezierCurve
{
/// <summary>
/// 线性公式
/// </summary>
Vector3 Bezier(Vector3 p0, Vector3 p1, float t)
{
return (1 - t) * p0 + t * p1;
}
/// <summary>
/// 二次方公式
/// </summary>
Vector3 Bezier(Vector3 p0, Vector3 p1, Vector3 p2, float t)
{
Vector3 p0p1 = (1 - t) * p0 + t * p1;
Vector3 p1p2 = (1 - t) * p1 + t * p2;
Vector3 result = (1 - t) * p0p1 + t * p1p2;
return result;
}
/// <summary>
/// 三次方公式
/// </summary>
Vector3 Bezier(Vector3 p0, Vector3 p1, Vector3 p2, Vector3 p3, float t)
{
Vector3 result;
Vector3 p0p1 = (1 - t) * p0 + t * p1;
Vector3 p1p2 = (1 - t) * p1 + t * p2;
Vector3 p2p3 = (1 - t) * p2 + t * p3;
Vector3 p0p1p2 = (1 - t) * p0p1 + t * p1p2;
Vector3 p1p2p3 = (1 - t) * p1p2 + t * p2p3;
result = (1 - t) * p0p1p2 + t * p1p2p3;
return result;
}
}
看了半天公式也转换成代码了,那么它到底用的呢?
看个例子:在Unity中绘制一条曲线

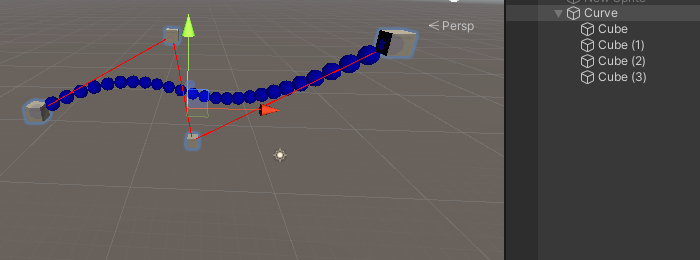
创建一个空物体作为父物体并挂载下面脚本,然后创建四个cube作为曲线控制点,即可在Scene视图下看到上图效果
using System.Collections;
using System.Collections.Generic;
using System.Linq;
using UnityEngine;
public class BezierCurveTest : MonoBehaviour
{
// 点的半径
public float radius = 1;
// 曲线取点的密度
public int densityCurve = 1000;
/// <summary>
/// 绘制曲线控制点 -- 此脚本的子物体
/// </summary>
public List<GameObject> ControlPointList = new List<GameObject>();
/// <summary>
/// 当前绘制曲线的所有点
/// </summary>
public List<Vector3> CurvePointList = new List<Vector3>();
/// <summary>
/// 编辑状态下子自动绘制曲线
/// </summary>
private void OnDrawGizmos()
{
// 绘制前重新添加控制点
ControlPointList.Clear();
foreach (Transform item in transform)
{
ControlPointList.Add(item.gameObject);
}
// Select 取每个点的position作为新的元素
List<Vector3> controlPointPos = ControlPointList.Select(point => point.transform.position).ToList();
// 经过三阶运算返回的需要绘制的点
var points = GetDrawingPoints(controlPointPos, densityCurve);
Vector3 startPos = points[0];
CurvePointList.Clear();
CurvePointList.Add(startPos);
for (int i = 1; i < points.Count; i++)
{
if (Vector3.Distance(startPos, points[i]) >= radius)
{
startPos = points[i];
CurvePointList.Add(startPos);
}
}
//绘制曲线
Gizmos.color = Color.blue;
foreach (var item in CurvePointList)
{
Gizmos.DrawSphere(item, radius * 0.5f);
}
//绘制曲线控制点连线
Gizmos.color = Color.red;
for (int i = 0; i < controlPointPos.Count - 1; i++)
{
Gizmos.DrawLine(controlPointPos[i], controlPointPos[i + 1]);
}
}
/// <summary>
/// 获取绘制点
/// </summary>
/// <param name="controlPoints"></param>
/// <param name="segmentsPerCurve"></param>
/// <returns></returns>
public List<Vector3> GetDrawingPoints(List<Vector3> controlPoints, int segmentsPerCurve)
{
List<Vector3> points = new List<Vector3>();
// 下一段的起始点和上段终点是一个,所以是 i+=3
for (int i = 0; i < controlPoints.Count - 3; i += 3)
{
var p0 = controlPoints[i];
var p1 = controlPoints[i + 1];
var p2 = controlPoints[i + 2];
var p3 = controlPoints[i + 3];
for (int j = 0; j <= segmentsPerCurve; j++)
{
var t = j / (float)segmentsPerCurve;
points.Add(CalculateBezierPoint(t, p0, p1, p2, p3));
}
}
return points;
}
// 三阶公式
Vector3 CalculateBezierPoint(float t, Vector3 p0, Vector3 p1, Vector3 p2, Vector3 p3)
{
Vector3 result;
Vector3 p0p1 = (1 - t) * p0 + t * p1;
Vector3 p1p2 = (1 - t) * p1 + t * p2;
Vector3 p2p3 = (1 - t) * p2 + t * p3;
Vector3 p0p1p2 = (1 - t) * p0p1 + t * p1p2;
Vector3 p1p2p3 = (1 - t) * p1p2 + t * p2p3;
result = (1 - t) * p0p1p2 + t * p1p2p3;
return result;
}
}
可以根据需求调整点的半径(radius )和曲线取点的密度(densityCurve )进行调整。

底图是我用系统内置的画图工具多段曲线拼接而成的。
根据上述示例,很容易想到在指定按照指定路径移动的情况下可以使用(比如:祖玛,保卫萝卜,塔防类)
下面这个Demo制作了一个可视化操作生成曲线点的工具;
实现原理:和二项中一致,我添加了一键保存配置文件扩展,它可以帮助你快速的实现关卡路径的制作,将所得的坐标点保存到本地文件,用的时候在拿出来用就可以了;
场景搭建:
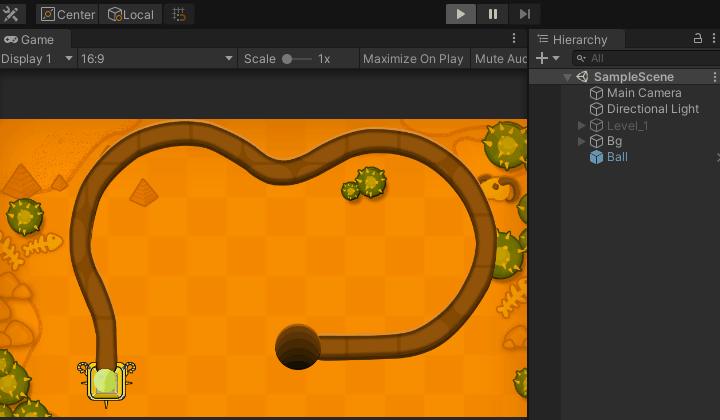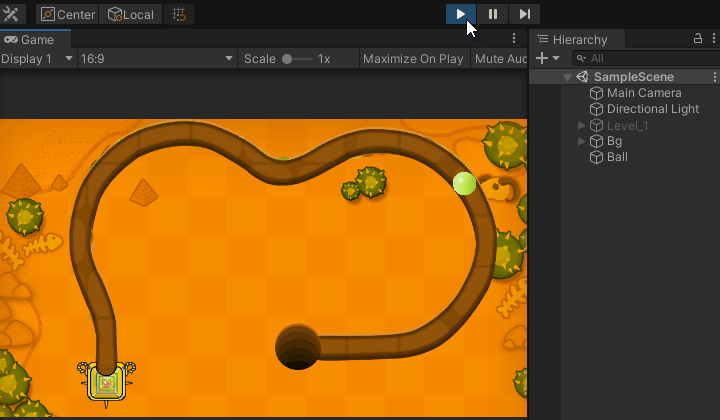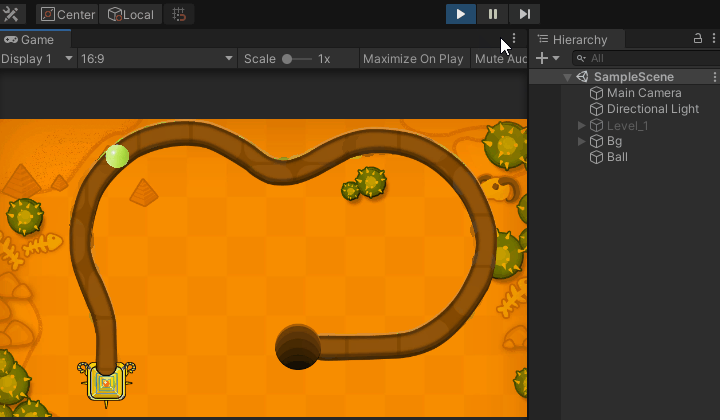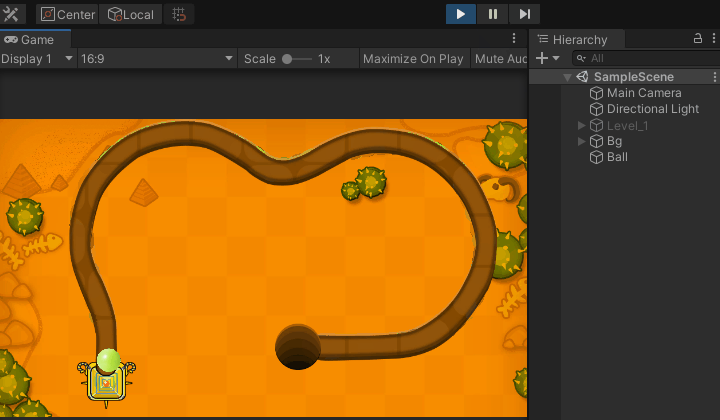
小球移动:
using UnityEngine;
using UnityEditor;
public class BallMove : MonoBehaviour
{
public MapConfig levelMapConfig;
public int AniMoveSpeed = 1;
float progress;
void Start()
{
progress = 0f;
if (levelMapConfig == null)
{
levelMapConfig = AssetDatabase.LoadAssetAtPath<MapConfig>("Assets/LevelMap/map_1.asset");
}
}
void FixedUpdate()
{
progress += Time.fixedDeltaTime * AniMoveSpeed;
transform.position = MovePosition();
}
// 获取下一个移动到的位置
Vector3 MovePosition()
{
if (levelMapConfig==null)
{
levelMapConfig = AssetDatabase.LoadAssetAtPath<MapConfig>("Assets/LevelMap/map_1.asset");
}
int index = Mathf.FloorToInt(progress);
if(index >= levelMapConfig.pathPointList.Count - 1)
{
index = 0;
progress = 0f;
}
return Vector3.Lerp(levelMapConfig.pathPointList[index], levelMapConfig.pathPointList[index + 1], progress - index);
}
}
制作地图路径脚本
using System.Collections.Generic;
using System.Linq;
using UnityEditor;
using UnityEngine;
/// <summary>
/// 制作地图路径脚本
/// </summary>
public class CreateBezierMapPathTools : MonoBehaviour
{
// 点的半径
public float radius;
// 曲线取点的密度
public int densityCurve;
/// <summary>
/// 绘制曲线控制点 -- 此脚本的子物体
/// </summary>
public List<GameObject> ConPointObjList = new List<GameObject>();
/// <summary>
/// 当前绘制曲线的所有点
/// </summary>
public List<Vector3> CurvePointList = new List<Vector3>();
/// <summary>
/// 编辑状态下子自动绘制曲线
/// </summary>
private void OnDrawGizmos()
{
// 绘制前重新添加控制点
ConPointObjList.Clear();
foreach (Transform item in transform)
{
ConPointObjList.Add(item.gameObject);
}
// Select 取每个点的position作为新的元素
List<Vector3> controlPointPos = ConPointObjList.Select(point => point.transform.position).ToList();
// 经过三阶运算返回的需要绘制的点
var points = GetDrawingPoints(controlPointPos, densityCurve);
Vector3 startPos = points[0];
CurvePointList.Clear();
CurvePointList.Add(startPos);
for (int i = 1; i < points.Count; i++)
{
if (Vector3.Distance(startPos, points[i]) >= radius)
{
startPos = points[i];
CurvePointList.Add(startPos);
}
}
//绘制曲线
Gizmos.color = Color.blue;
foreach (var item in CurvePointList)
{
Gizmos.DrawSphere(item, radius * 0.5f);
}
//绘制曲线控制点连线
Gizmos.color = Color.red;
for (int i = 0; i < controlPointPos.Count - 1; i++)
{
Gizmos.DrawLine(controlPointPos[i], controlPointPos[i + 1]);
}
}
/// <summary>
/// 获取绘制点
/// </summary>
/// <param name="controlPoints"></param>
/// <param name="segmentsPerCurve"></param>
/// <returns></returns>
public List<Vector3> GetDrawingPoints(List<Vector3> controlPoints, int segmentsPerCurve)
{
List<Vector3> points = new List<Vector3>();
// 下一段的起始点和上段终点是一个,所以是 i+=3
for (int i = 0; i < controlPoints.Count - 3; i += 3)
{
var p0 = controlPoints[i];
var p1 = controlPoints[i + 1];
var p2 = controlPoints[i + 2];
var p3 = controlPoints[i + 3];
for (int j = 0; j <= segmentsPerCurve; j++)
{
var t = j / (float)segmentsPerCurve;
points.Add(CalculateBezierPoint(t, p0, p1, p2, p3));
}
}
return points;
}
// 三阶公式
Vector3 CalculateBezierPoint(float t, Vector3 p0, Vector3 p1, Vector3 p2, Vector3 p3)
{
Vector3 result;
Vector3 p0p1 = (1 - t) * p0 + t * p1;
Vector3 p1p2 = (1 - t) * p1 + t * p2;
Vector3 p2p3 = (1 - t) * p2 + t * p3;
Vector3 p0p1p2 = (1 - t) * p0p1 + t * p1p2;
Vector3 p1p2p3 = (1 - t) * p1p2 + t * p2p3;
result = (1 - t) * p0p1p2 + t * p1p2p3;
return result;
}
// 保存当前编辑器下的关卡地图文件
public void SaveLevelMapAsset()
{
string assetPath = "Assets/LevelMap/map_" + name.Substring(name.Length - 1) + ".asset";
MapConfig mapConfig = ScriptableObject.CreateInstance<MapConfig>();
foreach (var item in CurvePointList)
{
mapConfig.pathPointList.Add(item);
}
MapConfig config = AssetDatabase.LoadAssetAtPath<MapConfig>(assetPath);
if (config)
{
AssetDatabase.DeleteAsset(assetPath);
}
AssetDatabase.CreateAsset(mapConfig, assetPath);
AssetDatabase.SaveAssets();
Debug.Log("地图文件保存成功,保存路径为:" + assetPath);
}
}
[CustomEditor(typeof(CreateBezierMapPathTools))]
public class BezierEditor : Editor
{
public override void OnInspectorGUI()
{
base.OnInspectorGUI();
if (GUILayout.Button("保存地图文件"))
{
(target as CreateBezierMapPathTools).SaveLevelMapAsset();
}
}
}
Demo 下载地址:
分享名称:BezierCurveDemo.unitypackage
分享链接:https://pan.hackyin.com/#s/8plUu7IQ
访问密码:gzMT1